[java] 프로그래머스 - 삼각 달팽이

문제

프로그래머스-삼각 달팽이
밑변의 길이와 높이가 n인 삼각형에서 달팽이 채우기를 진행한 후, 첫 행부터 마지막 행까지 숫자를 합친 배열을 리턴하는 문제

• 제한 사항
  n은 1이상 1,000 이하다

• 예시
  
  n = 4 인 경우, 위에서부터 순서대로 배열에 적용하면
  [1,2,9,3,10,8,4,5,6,7] 가 된다

풀이

삼각형에서 규칙을 찾아서 배열에 적용하면 된다
규칙찾는게 수포자에게는 힘들 뿐.. ㅎ
먼저 답을 구하기 위해 생각해봐야 할 것을 정리하자면

1. 전체 배열의 크기
2. 왼쪽 대각선 채울 때 idx 규칙(시작 idx)
   ( 밑변채우는건 쉬우니까 패스)
3. 오른쪽 대각선 채울 때 idx 규칙
4. 내부 삼각형의 값을 어떻게 채울지
   (아래 설명은 N=10삼각형을 기준으로 되어있음)

🥊 문제풀이 참고용 N=10 삼각형

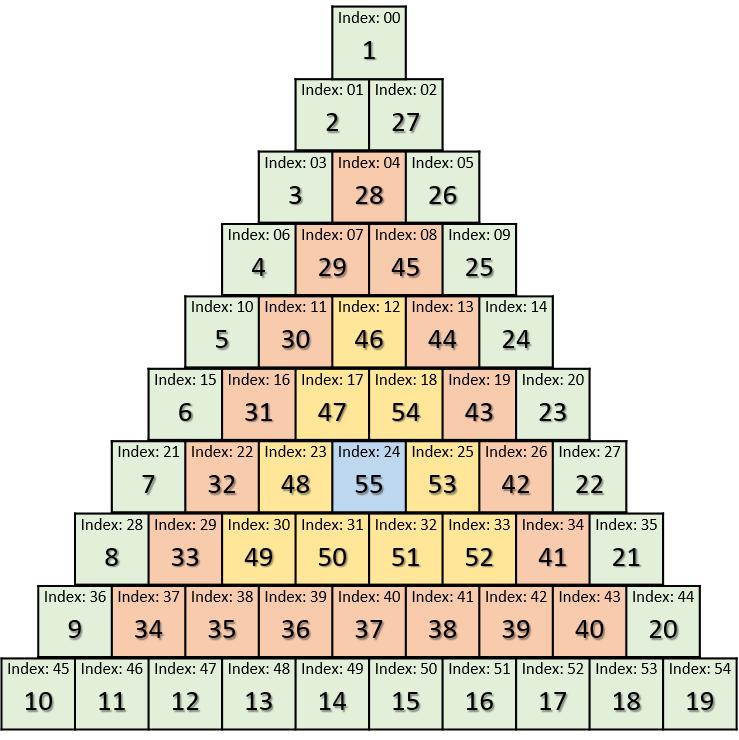
🥊 전체 배열의 크기

삼각형 밑변 길이를 가지고 전체 배열의 크기는 어떻게 구할 수 있을까?

N	전체 배열의 크기
4	10
5	15
6	21

n * (n + 1) / 2
n = 6인 경우, [1 + 2 + 3 + 4 + 5 + 6]이므로 1 ~ 6의 합이기 때문

🥊 왼쪽 빗변

삼각형을 채우기 시작할 때 배열의 몇번째 인덱스부터 시작해야할까?
처음에 제일 큰 삼각형, 가장 외부에 있는 삼각형(길이 : N)을 그릴땐 0부터 시작하지만
내부 삼각형을 그릴때에도 0부터 시작할 순 없다

변수 k를 줘서 외부에서부터 몇번째 겹(layer)인지를 저장한다

(위에 예시그림에서 색상이 조금 더 짙어짐)

색상	k	시작 인덱스
녹색	0	0
주황	1	4
노랑	2	12
파랑	3	24

시작 인덱스 : 2k(k + 1)

시작인덱스부터 n-1회 값을 채운다(밑변 제외)
이때의 인덱스에도 규칙을… 찾아..

먼저 인덱스가 어떻게 변화하는지 보자

색상	k	시작 인덱스	인덱스의 변화
녹색	0	0	0 1 3 6 10 15 21 28 36 45
주황색	1	4	4 7 11 16 22 29 37
노랑색	2	12	12 17 23 30
파랑색	3	24	24

시작 인덱스부터 값이 증가하는 데 이 수열에서 규칙은??

색상	k	시작 인덱스	인덱스의 변화	계차 시작 값
녹색	0	0	0 1 3 6 10 15 21 28 36 45	1
주황색	1	4	4 7 11 16 22 29 37	3
노랑색	2	12	12 17 23 30	5
파랑색	3	24	24

(화살표 -> 시작인덱스)

• 녹색
  

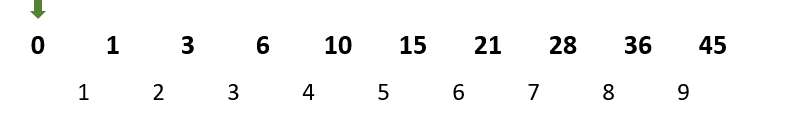
• 노랑색
  

시작 인덱스에서 더해지는 첫번째 값(=계차 시작 값) : 2k + 1

🥊 오른쪽 빗변

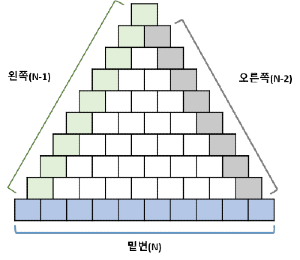
왼쪽 빗변(대각선) 채울 때 인덱스가 계차 수열로 되어있는데
오른쪽 빗변의 인덱스는 증가가 아닌 감소 형태로 되어있다
또한 왼쪽 채울때 n-1회하면서 밑변을 제외했는데
마찬가지로 삼각형의 첫번째 칸과 밑변을 제외하면서 n-2가 된다

색상	k	N	감소 횟수(N-2)	밑변 마지막 인덱스	(앞으로)채워야 하는 오른쪽 인덱스
녹색	0	10	8회	54	44 35 27 20 14 9 5 2
주황색	1	7	5회	43	34 26 19 13 8
노랑색	2	4	2회	33	25 18
파랑색	3	1

밑변채울때 가장 마지막으로 채웠던 ‘밑변 마지막 인덱스’부터 채워 나갈 인덱스까지,
이때도 일정한 규칙이 있다

sn : 내부 삼각형 길이 (sn <= N)
N : 가장 큰 삼각형 길이, (여기서는 N = 10)

색상	k	삼각형 길이(sn)	감소 횟수(N-2)	밑변 마지막 인덱스	(앞으로)채워야 하는 오른쪽 인덱스	계차 시작 값
녹색	0	10	8회	54	44 35 27 20 14 9 5 2	-10
주황색	1	7	5회	43	34 26 19 13 8	-9
노랑색	2	4	2회	33	25 18	-8
파랑색	3	1

(화살표 -> 밑변의 마지막 인덱스)

• 녹색
  

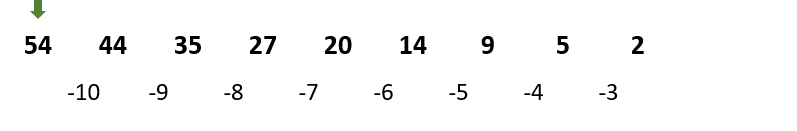
• 주황색
  

계차 시작 값 : (N - k) * - 1 (이때의 N은 가장 큰 삼각형 길이)

색상	계차 시작 값
녹색	(10 - 0) * -1 = -10
주황색	(10 - 1) * -1 = -9
노랑색	(10 - 2) * -1 = -8

🥊 내부 삼각형 크기

삼각형의 밑변 길이를 N
삼각형 내부 작은 삼각형 밑변 길이를 sn이라고 하자

색상	k	sn
녹색	0	10
주황색	1	7
노랑색	2	4
파랑색	3	1

sn(N의 내부 삼각형 길이) : N - 3k
그냥 반복문에서 처음에 입력받은 N을 3씩 빼주면 됨..
sn이 0보다 클때까지 감소하면서 삼각형을 채우면 된다

소스코드

class Solution {
static int[] answer;
	static int value;
	static int N;

	public int[] solution(int n) {
		N = n;
		answer = new int[n * (n + 1) / 2];
		value = 1; // 채워넣을 값, 전역변수
		int k = 0; // 겹
		while (n >= 1) {
			fillArr(2 * k * (k + 1), 2 * k + 1, n, k);
			n -= 3; // 내부 삼각형 크기
			k++;
		}
		return answer;
	}

	// 파라미터 : 시작인덱스, 왼쪽빗변 계차 시작값, 길이 n, 겹 k
	private void fillArr(int startIdx, int sub, int n, int k) {

		if (n == 1) {
			answer[startIdx] = value;
			return;
		}
		// / __ \ 순으로 숫자 채우기
		
		// / 왼쪽 대각선
		int idx = startIdx;
		int cnt = n - 1; // 밑변을 제외한 횟수
		while (cnt > 0) {
			answer[idx] = value++;
			idx += sub++;
			cnt--;
		}
		// ㅡ 밑변
		for (int i = 0; i < n; i++) {
			answer[idx++] = value++;
		}
		// \ 오른쪽 대각선
		idx--;
		int nk = N - k; // 계차 시작값, -1을 곱하는 대신 (-=)처리
		for (int i = 0; i < n - 2; i++) {
			idx -= nk;
			answer[idx] = value++;
			nk--;
		}
	}
}