[java] 프로그래머스 - 섬 연결하기

문제

프로그래머스-섬 연결하기
n개의 섬 사이에 다리를 건설하는 비용이 주어질 때 최소의 비용으로 모든 섬을 연결하는 가격을 구하는 문제
모든 섬 사이의 다리 건설비용이 주어지는 것은 아님(이 경우, 두 섬을 잇는 다리는 없음)
연결할 수 없는 섬은 주어지지 않음
두 섬을 연결하는 다리에는 방향성이 존재하지 않음

• 예시
  
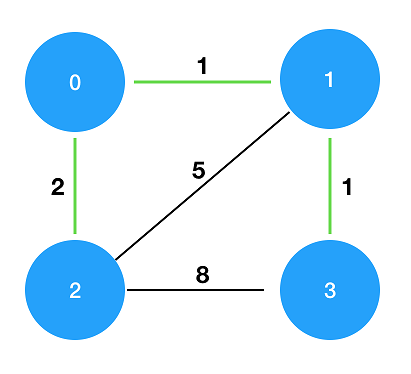
  그림과 같이 섬과 다리건설 비용이 주어지는 경우, 초록색으로 연결하는 것이 가장 적은비용으로 모든 섬을 잇는 방법

풀이

크루스칼 알고리즘으로 풀었다
1) 다리의 연결 정보와 비용을 객체로 저장 후 정렬
우선 비용이 최소여야 하므로 다리의 연결정보와 비용을 객체로 만들어서 우선순위 큐에 저장했다.

2) union-find를 적용하기 위해 준비
union-find에서 필요한 부모 정보를 저장하기 위한 배열(chk)을 만들고 인덱스를 저장한다.

3) 최소 비용 순으로 다리 정보를 뽑으면서 연결된 두 섬이 연결되었는지 확인한다
두 섬이 연결되어있으면 건너뛰고, 연결되어있지 않으면 연결해준다
연결 시 비용을 추가해준다

소스코드

import java.util.PriorityQueue;

class Solution {
	static int chk[];

	public int solution(int n, int[][] c) {
		int answer = 0;
		// 1) 객체 생성 후 pq에 저장  
		PriorityQueue<Road> pq = new PriorityQueue<>();
		for (int i = 0; i < c.length; i++) {
			int ia = c[i][0];
			int ib = c[i][1];
			pq.add(new Road(ia, ib, c[i][2]));

		}
		// 2) chk배열 선언 후 i번째에는 i를 넣어줌(초기화)
		chk = new int[n];
		for (int i = 0; i < chk.length; i++) {
			chk[i] = i;
		}
		while (!pq.isEmpty()) {
			Road curr = pq.poll();
			// 3) 두 섬이 연결되어있지 않으면 두 섬을 이어줌, 비용 추가
			if (find(curr.x) != find(curr.y)) {
				union(curr.x, curr.y);
				answer += curr.cost;
			}
		}
		return answer;
	}

	private void union(int x, int y) {
		int p = find(x);
		int q = find(y);
		chk[p] = q;

	}

	private int find(int x) {
		if (chk[x] == x)
			return x;
		return find(chk[x]);
	}

}

class Road implements Comparable<Road> {
	int x;
	int y;
	int cost;

	public Road(int x, int y, int cost) {
		super();
		this.x = x;
		this.y = y;
		this.cost = cost;
	}

	@Override
	public int compareTo(Road r) {
		// TODO Auto-generated method stub
		return this.cost - r.cost;
	}
}