[java] 세그먼트 트리 자료구조

세그먼트 트리 구조 개념 및 코드

개념

세그먼트 트리(Segment Tree)는 기본적으로 단편, 구분을 저장하는 데 사용되는 이진트리이다
세그먼트 트리의 각 리프는 단일 요소를 나타낸다
세그먼트 트리의 내부 노드는 기본 간격의 합집합을 나타낸다

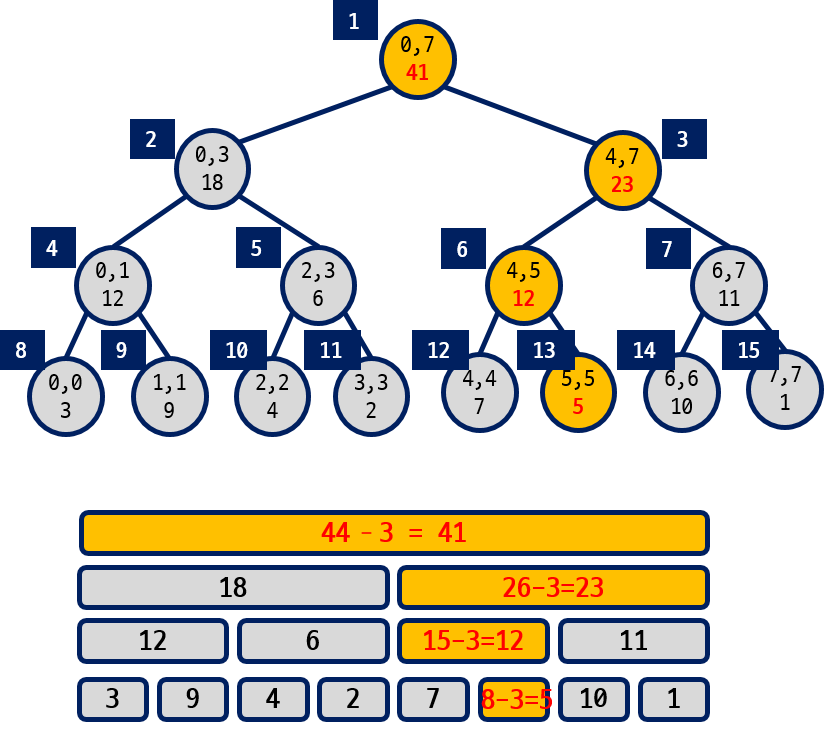
최상단 노드는 [0,7]처럼 0번 리프부터 7번 리프의 합을 가지고 있다
하위 두 노드의 값을 루트가 가지고 있는 형태를 띄고 있다

세그먼트 트리가 구축되면 구조를 변경할 수 없다
노드값을 업데이트 할 수 있지만, 구조는 변경할 수 없다

세그먼트 트리는 인덱스가 1부터 시작하는게 통상적이다
최상단 노드의 인덱스가 k이면 2k는 k의 왼쪽 자식노드를 가리키므로 효과적이기 때문이다

특징

• 노드의 왼쪽 하위트리에는 해당 노드의 값보다 작은 값을 지닌 노드로 이루어져있다
• 노드의 오른쪽 하위트리에는 해당 노드의 값보다 큰 값을 지닌 노드로 이루어져 있다
• 단일 요소가 N개일 때, 세그먼트 트리를 이루는 총 노드의 수는 (Full Binary Tree 기준)
  • N이 2의 제곱꼴일때 -> 2*N-1개
  • N이 2의 제곱꼴이 아닐때 -> 2^(H+1)-1개 (H = 높이, log2N)

코드

배열 크기 지정

int input[] = { 5, 8, 7, 3, 1, 3, 2, 7, 9, 7 };
int N = input.length;
int h = (int) Math.ceil(Math.log(N) / Math.log(2)); // log2(N)
int size = (int) Math.pow(2, h + 1); // -1을 하지않는 이유는 1부터 시작하기 위해서 
long tree[] = new long[size];

초기화

최상단 인덱스(1)에서 재귀를 이용해 값을 채우는 방법이다

init(1, 0, N-1)
1 : 세그먼트트리 시작인덱스
0 : 입력할 배열의 시작인덱스
N-1 : 입력할 배열의 마지막 인덱스

private static long init(int node, int start, int end) {
	if (start == end) // 리프노드(단일원소값인 경우)
		return tree[node] = input[start];

	int mid = (start + end) / 2;
	return tree[node] = init(node * 2, start, mid) + init(node * 2 + 1, mid + 1, end);
}

구간 합 찾기

구해야 하는 범위를 [left, right]라고 하고, 노드가 담당하는 구간이 [start, end]라고 하자
최상단 노드의 담당구간 [start, end] 는 [0, N-1]이다

이 때 다음과 같이 4가지 경우로 나눌 수 있다

1. [left,right]와 [start,end]가 겹치지 않는 경우
2. [left,right]가 [start,end]를 완전히 포함하는 경우
3. [start,end]가 [left,right]를 완전히 포함하는 경우
4. [left,right]와 [start,end]가 겹쳐져 있는 경우 (1, 2, 3 제외한 나머지 경우)

• 1. [left,right]와 [start,end]가 겹치지 않는 경우
  이 경우에는 if( left > end || right < start )로 나타낼 수 있다
  이때는 겹치지 않기때문에 탐색을 이어나가지않고 0을 리턴해서 종료한다

• 2. [left,right]가 [start,end]를 완전히 포함하는 경우
  이 경우에는 if( left <= start && end <= right )로 나타낼 수 있다
  구해야 하는 범위는 left ~ right인데 start ~ end는 해당 범위에 완전히 포함되고, start~end의 하위노드들도 모두 포함이기 때문에 탐색을 진행할 필요가 없다. tree[node]를 리턴해서 종료한다

• 3. [start,end]가 [left,right]를 완전히 포함하는 경우
  4. [left,right]와 [start,end]가 겹쳐져 있는 경우 (1, 2, 3 제외한 나머지 경우)
  두 경우에는 왼쪽 자식노드와 오른쪽 자식노드를 루트로 하는 트리에서 다시 탐색을 시작해야 한다

• 💎 3 ~ 6 까지 구간합을 구할 때

  sum(1, 0, N-1, 3, 6)
  1 : 세그먼트트리 시작인덱스
  0 : 입력할 배열의 시작인덱스
  N-1 : 입력할 배열의 마지막 인덱스
  3 : 합을 구할 구간의 첫번째 원소 인덱스
  6 : 합을 구할 구간의 마지막 원소 인덱스

private static long sum(int node, int start, int end, int left, int right) {
	if (left > end || right < start)
		return 0;
	if (left <= start && end <= right)
		return tree[node];

	int mid = (start + end) / 2;
	return sum(node * 2, start, mid, left, right) + sum(node * 2 + 1, mid + 1, end, left, right);
}

수 변경하기

중간에 어떤 수를 변경하면, 해당 수가 포함된 구간을 담당하는 노드를 모두 변경해야 한다

예시 그림에서 5번째 원소를 변경한다고 하면, 주황색으로 칠해진 부분을 수정해줘야한다

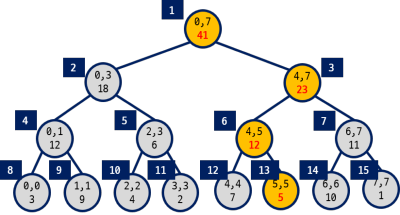
이 때, 원소 값과 변경하려는 값의 차이를 diff라고 할 때, 이 diff를 변경하려는 원소의 구간합 계산구간에 적용해줘야한다
5번째 원소 5를 7로 변경한다고 하면, diff = 2이다
노랗게 칠해진 구간에 이 diff를 적용해주면 된다

• 💎 5번째 원소를 7로 변경할 때

  update(1, 0, N-1, 5, 2)
  1 : 세그먼트트리 시작인덱스
  0 : 입력할 배열의 시작인덱스
  N-1 : 입력할 배열의 마지막 인덱스
  5 : 변경할 원소의 인덱스
  2 : 기존 원소와 변경할 원소의 diff값

private static void update(int node, int start, int end, int index, int diff) {
	if (index < start || index > end) // 인덱스 범위 조정
		return;
	tree[node] += diff; // diff 변경 적용
	if (start != end) {
		int mid = (start + end) / 2;
		update(node * 2, start, mid, index, diff);
		update(node * 2 + 1, mid + 1, end, index, diff);
	}
}

전체 코드(github)

github - commit

풀 수 있는 문제

관련해서 풀만한 문제 몇개 총총
백준 - 구간 합 구하기
백준 - 구간 곱 구하기
백준 - 최솟값과 최댓값

참고

41. 세그먼트 트리(Segment Tree)
세그먼트 트리(Segment Tree)
[알고리즘] 세그먼트 트리 ( Segment Tree )