[java] 이진탐색트리(BST) 자료구조

이진탐색트리(BST) 자료구조 개념 및 코드

개념

이진 탐색 트리(Binary Search Tree는 노드 기반의 이진 트리 자료구조

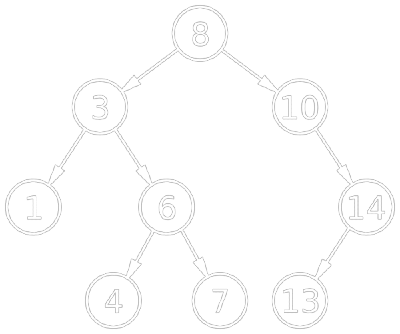
특징

• 노드의 왼쪽 하위트리에는 해당 노드의 값보다 작은 값을 지닌 노드로 이루어져있다.
• 노드의 오른쪽 하위트리에는 해당 노드의 값보다 큰 값을 지닌 노드로 이루어져 있다.

코드

기본 구조

Node Class

• 숫자값 : key
• 왼쪽 노드 : left
• 오른쪽 노드 : right

  class Node {
    int key;
    Node left;
    Node right;
  
    public Node(int value) {
        key = value;
        left = null;
        right = null;
    }
  
    public Node(int value, Node leftChild, Node rightChild) {
        super();
        this.key = value;
        this.left = leftChild;
        this.right = rightChild;
    }
  }
  

BinarySearchTree

• 루트노드 : root

  class BinarySearchTree {
    Node root;
    public BinarySearchTree() {
        root = null;
    }
  

  root노드를 가지고 있으며 초기값은 null이다

insert

void insert(int key) {
	root = insertRec(root, key);
}

Node insertRec(Node root, int key) {
	if (root == null) {
		root = new Node(key);
		return root;
	}

	if (key < root.key) {
		root.left = insertRec(root.left, key);
	} else if (key > root.key) {
		root.right = insertRec(root.right, key);
	}
	return root;

}

1. root가 없는경우(null), root에 삽입하려는 노드를 생성해서 저장한다
2. root가 있는경우, 삽입하려는 key값을 root의 왼쪽/오른쪽 자식노드의 값과 비교한다.
   해당 자식 노드를 기준으로 1단계로 돌아가서 반복한다
3. root를 반환

find

public boolean find(int key) {
	return findRec(root, key);
}

private boolean findRec(Node curr, int key) {
	if(curr == null)
	return false;
	if(key < curr.key)
		return findRec(curr.left, key);
	else if(key > curr.key)
		return findRec(curr.right, key);
	else if(key== curr.key)
		return true;
	
	return false;
}

1. 재귀형태로 curr노드에서 key값을 비교하며 진행한다
2. 만일 key가 curr노드의 왼쪽/오른쪽보다 크다면 curr의 오른쪽/왼쪽자식노드로 진행,
   key가 curr의 값과 같으면 찾았으므로 true리턴
   진행 시 null인 경우 false를 리턴한다

delete

public void deleteKey(int key) {
	root = deleteRec(root, key);
}

private Node deleteRec(Node curr, int key) {
	if (curr == null)
		return curr;
	if (key < curr.key)
		curr.left = deleteRec(curr.left, key);
	else if (key > curr.key)
		curr.right = deleteRec(curr.right, key);
	else {
		// node with only child or null
		if (curr.left == null)
			return curr.right;
		else if (curr.right == null)
			return curr.left;

		// node with two children : get smallest value in right subtree
		curr.key = minValue(curr.right);
		curr.right = deleteRec(curr.right, curr.key);
	}
	return curr;
}

• 삭제할 노드가 자식노드가 없는경우
  1. root부터 시작해서 삭제할 값(key)를 비교해서 왼/오 방향의 자식노드로 내려간다.
  2. 삭제하려는 노드를 찾은 경우, 해당노드의 오른쪽 자식노드(null)를 상위 노드의 오른쪽노드로 지정한다.
     5-6-7 순의 노드가 있다고 가정했을 경우, 7을 삭제한다면
     7의 하위오른쪽노드는 null이므로 이때 6의 오른쪽노드를 null로 등록한다 -> 7이 사라짐
• 삭제할 노드가 자식노드(왼/오)가 1개있는 경우
  1. root부터 시작해서 삭제할 값(key)를 비교해서 왼/오 방향의 자식노드로 내려간다.
  2. 왼쪽노드가 null인 경우, 오른쪽 노드를 상위 노드에게 리턴한다.
     오른쪽 노드가 null인 경우, 왼쪽 노드를 상위 노드에게 리턴한다.
     5-6-7 의 노드가 있다고 가정할 경우, 6을 삭제한다면
     6의 하위 오른쪽노드는 7이고 이때 왼쪽은 null이므로 7노드를 리턴한다.
     5에서 right노드를 7로 등록한다 -> 6이 사라짐
• 삭제할 노드가 자식노드(왼/오)가 둘다 경우
  1. root부터 시작해서 삭제할 값(key)를 비교해서 왼/오 방향의 자식노드로 내려간다.
  2. 현재 노드의 오른쪽 노드 중 가장 작은값을 현재 노드의 값(key)로 지정한다.
  3. 우측 서브트리에서 가장 작은 값을 삭제한다.
     6-5(root)-9의 경우, 5를 삭제할 때 우측에서 가장 작은값은 9이다. 5의 값을 9로 교체하고, 9를 제거한다. 6-5(root)

minValue

• 노드 삭제 진행 시 하위(왼,오) 노드가 둘다 존재하는 노드를 삭제해야할 경우
  새로운 root를 등록해야하므로 왼쪽으로 진행하면서 가장 작은값을 찾아 root로 변경하기위해 필요한 함수

    private int minValue(Node curr) {
        int minv = curr.key;
        while (curr.left != null) {
            minv = curr.left.key;
            curr = curr.left;
        }
        return minv;
    }
  

print(inOrder)

public void inOrder() {
	inOrderRec(root);

}

private void inOrderRec(Node curr) {
	if (curr != null) {
		inOrderRec(curr.left);
		System.out.println(curr.key);
		inOrderRec(curr.right);
	}

}

재귀형태로 순환하면서 왼쪽하위노드 - 루트노드 -오른쪽하위노드 순으로 중위순회하는 방법
전위 순회 : 노드 - 왼쪽 - 오른쪽
후위 순회 : 왼쪽 - 오른쪽 - 노드

전체 코드(github)

github - commit

풀 수 있는 문제

관련해서 풀만한 문제 몇개 총총
프로그래머스 - 입국심사
백준 - 휴게소 세우기

참고

wikipedia 이진탐색트리
Binary Search Tree - GeeksforGeeks
Binary Search Tree | Set 1 (Search and Insertion)
Binary Search Tree | Set 2 (Delete)

같이보면 좋을 것들

Red-Black Tree | Set 1 (Introduction)
Red-Black Tree